task/30277512 см ПРИЛОЖЕНИЕ
Модуль "АЛГЕБРА"
ответы : 21. x = 5. 22. v = [33] 21 /23
23. m = - 6,25 , m = 12,25.
Модуль "ГЕОМЕТРИЯ"
2 4. Дано : ∡B =66° , ∡C =84° , R =15 . || а = BC - ?
" решение" По теореме синусов : a/sin(∡A) =2R ⇒a =2Rsin(∡A) ,∡A =180°- (∡B+∡C)=180°-(66°+84°) =180°-150°=30°. a =2*15*sin30°=2*15*1/2 =15.
ответ : 15.
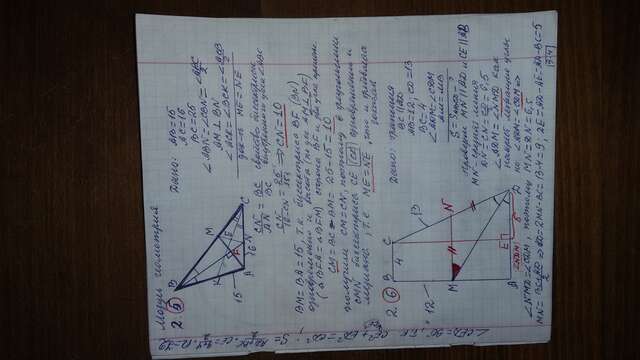
2 6. Дано : трапеция ABCD ; AB =12 ,CD = 13 , BC || AD , BC= 4 , ∡ADM =∡CDM , M ∈ AB , AM = BM . S(ABCD) = S - ?
решение Проведем MN || BC ( N ∈ CD ) и СE || BA ( E ∈ AD )
MN → средняя линия трапеции S = NM*H , где H высота трапеции
∡ADM =∡DMN ( накрест лежащие углы) , но ∡ADM= ∡CDM, значит ∡DMN = ∡CDM и как следствие ΔDNM равнобедренный :
NM=ND=BC/2=13/2= 6,5. NM =(AD+BC)/2⇒AD=2MN-BC=9
ABCE параллелограмм.EC=AB=12, ED =AD-AE=AD-BC=9-4 =5 .
По обратной теореме Пифагора заключаем,что ∡DEC=90° ( CE⊥AD, ΔDEC прямоугольный) , действительно: EC²+ ED²=12²+ 5²=144+25 =169 =13² =CD² * * * 5 ; 12; 13 _ Пифагорова тройка * * *
S = NM*H = 6,5*12= 78
ответ : 78