Ребят, помогите с геометрией, 9 класс, пожалуйста! Дам прилично баллов, только без спама,...

Question

Ребят, помогите с геометрией, 9 класс, пожалуйста! Дам прилично баллов, только без спама, прошу!И с пояснениями, пжлст

---

Answer 1

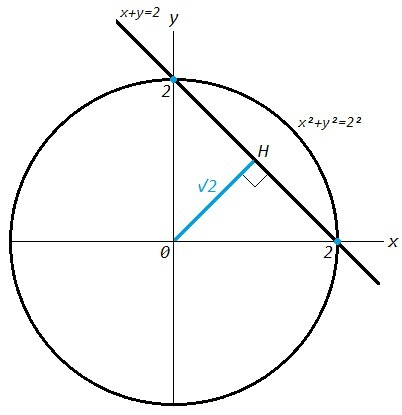
Уравнение x^2 +y^2 =4 задает окружность радиусом 2 с центром в начале координат. Окружность проходит через точки (0;2), (2;0).

Уравнение x+y =2 задает прямую, проходящую через точки (0;2), (2;0).

Прямая пересекает окружность, найдены две общие точки (прямая и окружность имеют не более двух общих точек).

Расстояние OH от центра окружности до прямой найдем из равнобедренного прямоугольного треугольника с катетами 2 как высоту из прямого угла.

ОН= √2

---

Comments

Если центр окружности в начале координат, то уравнение окружности x^2 +y^2 =r^2 (теорема Пифагора, где катеты - координаты x, y, гипотенуза - радиус).