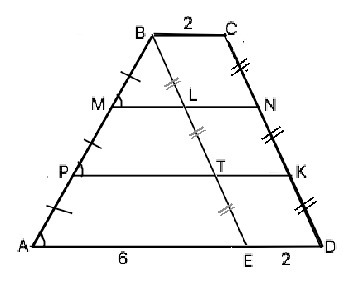
Возможно. к рисунку указано, что АВСD- трапеция. Если прямые, пересекающие две другие прямые, отсекают на обеих из них равные (или пропорциональные) между собой отрезки, то такие прямые параллельны (следствие из т.Фалеса). АВСD – трапеция.
Прямые РК, MN и ВС отсекают на АВ и СD равные отрезки ⇒ ВС║MN║PK║AD.
Проведем прямую параллельно СD до пересечения с AD в точке Е. ВСDE - параллелограмм по определению.⇒ ЕD=2; ⇒ АЕ=6. По условию ВМ=МР=РА. ⇒ АВ=3ВМ
Рассмотрим ∆ АВЕ и ВМL. Они подобны по двум углам: соответственные углы при МL и АЕ равны по свойству параллельных прямых и секущей, угол В - общий. k=МВ:АЕ=ВМ:ВА=
⇒ МL:АЕ= ⇒ ML=6:3=2. МN=ML+LN. Т.к. ВС║MN, и ВЕ║CD, LN=BC, то МN=4.
РК соединяет середины боковых сторон трапеции AMND ⇒ РК – её средняя линия и равна полусумме МN+AD=(4+8):2=6
