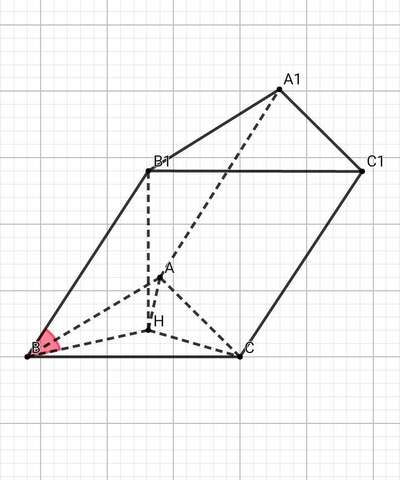
Основанием наклонной треугольной призмы есть правильный треугольник. Если боковое ребро призмы имеет длину 8 см и наклонено к плоскости основания под углом 30°, а одна из вершин призмы проектируется в центр нижнего основания, то чему равен объем призмы?
РЕШЕНИЕ:
• Рассмотрим тр. В1ВН (угол В1НВ = 90°):
sin30° = B1H/BB1 => B1H = BB1 • sin30° = 8 • 1/2 = 4 см
cos30° = BH/BB1 => BH = BB1 • cos30° = 8 • V3/2 = 4V3 см
• Рассмотрим тр. АВС ( равносторонний ):
BH = R = 4V3
AB = a = V3R = V3 • 4V3 = 4 • 3 = 12 см
AB = BC = AC = 12 см
• Обьём прямой призмы равен:
V = S осн. • h = S abc • B1H = ( a^2 • V3 / 4 ) • 4 = ( 12^2• V3 / 4 ) • 4 = 144V3
ОТВЕТ: 144V3