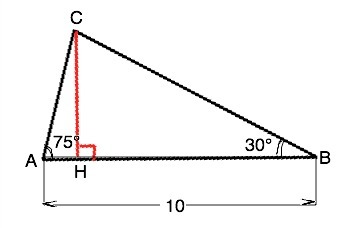
В треугольнике ABC угол А=75°, угол В=30°. Сумма углов треугольника 180°, следовательно, угол С=180°-30°-75°=75°. Углы при стороне АС равны => ∆ АВС равнобедренный, ВС=ВА=10 см.
Опустим из вершины угла С высоту СН на сторону АВ. Треугольник СВН прямоугольный. Катет СН противолежит углу 30° и по свойству такого катета равен половине гипотенузы ВС=5 см.
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. S=CH•AB:2=5•10:2=25 см²