ПОМОГИТЕ ** ФОТО

Question

ПОМОГИТЕ НА ФОТО

---

Answer 1

Окружность с центром О не только вписанa в угол ВАС, но она вписана и в угол АNH. Поэтому по теореме об отрезках касательных: отрезки касательных, к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Следовательно, угол ANO = угол HNO. Но с другой стороны, NH || AO - по условию => угол НNO = угол АОN - как накрест лежащие углы при NH || AO и секущей NO. Отсюда угол ANO = угол AON => тр. AON - равнобедренный, AN = AO = 7


ОТВЕТ: 7

---

Answer 2

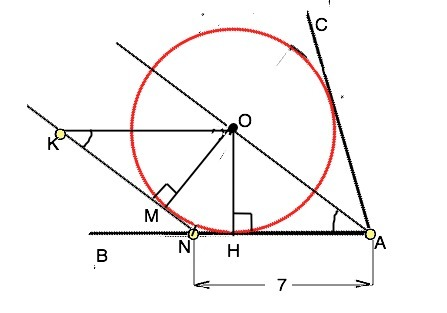
 Проведем к точкам касания на АВ и прямой, параллельной АО, радиусы ОН и ОМ соответственно. Они равны и перпендикулярны касательным (свойство). Из центра О проведем параллельно АВ прямую до пересечения с касательной  в точке К. ОК║AN; NK║АО. Четырехугольник ANOK - параллелограмм.

 Отрезки NM и NH равны по свойству касательных из одной точки. Прямоугольные ∆ КОМ=∆ АОН по катету ( ОМ=ОН - радиусы) и острому углу ∠К=∠А (противоположные углы параллелограмма). Следовательно, АО=КО (гипотенузы равных треугольникоа), а КО=АN (противоположные стороны параллелограмма). ⇒ АО=AN=7 (ед. длины)

---

Comments

:)