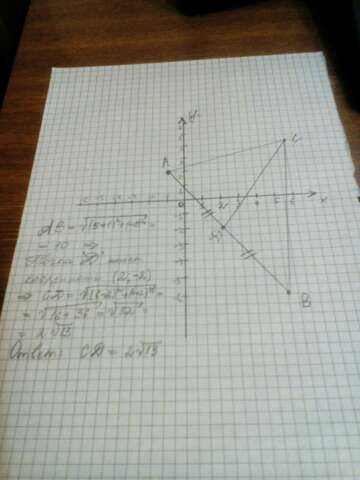
Дано:
А(-1;2) , B(5:-6), C(6;4)
Найти: CD
Решение:
1) Т.к. CD - медиана, то точка D будет серединой отрезка AB , поскольку из вершины С к стороне AB идёт отрезок, делящий её пополам. => AD=DB
2) Обозначим на координатной плоскости точки A,B,C с их координатами и соединим их отрезками.
3) найдём длину AB и поделки её пополам, чтобы найти середину отрезка и обозначим точку D
AB = √((5+1)^2 + (-8)^2) = √(36+64) = √100 = 10
D имеет координаты по X суммы B(x) + A(x) , делённое на два и Y суммы B(y) + A(y) , делённое на два. Получается D X= (5-1)/2 ; Y= (-6+2)/2 => D(2;-2)
4) CD = √((6-2)^2 + (4+2)^2) = √(16+36) = √52 = √4*13 = 2√13
Ответ: 2√13
К этому решению также приведен чертеж на фотографии.