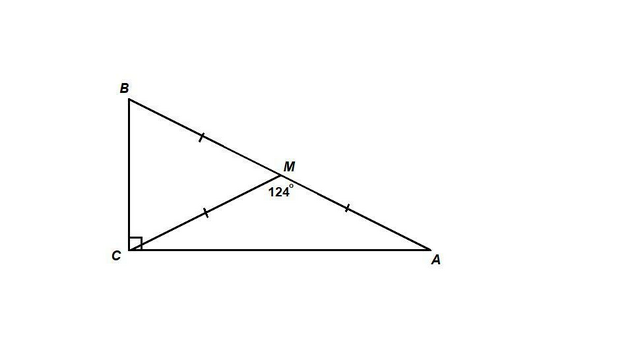
В прямоугольном треугольнике ABC СМ - медиана, проведенная к гипотенузе AB. Найдите величину большего острого угла треугольника АВС, если угол АМС равен 124°.
Ответ: 62°
Объяснение:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине:
АМ = СМ = ВМ.
ΔАМС равнобедренный, углы при основании равны:
∠МАС = ∠МСА = (180° - 124°) / 2 = 28°.
Сумма острых углов прямоугольного треугольника равна 90°, значит
∠В = 90° - ∠МАС = 90° - 28° = 62° - больший острый угол.