СРОЧНО! Постройте график функции (на картинке) . При каких значениях аргумента значения...

$\sf y=\dfrac{x^2-3x}{x-3}=\dfrac{x(x-3)}{x-3}=x$

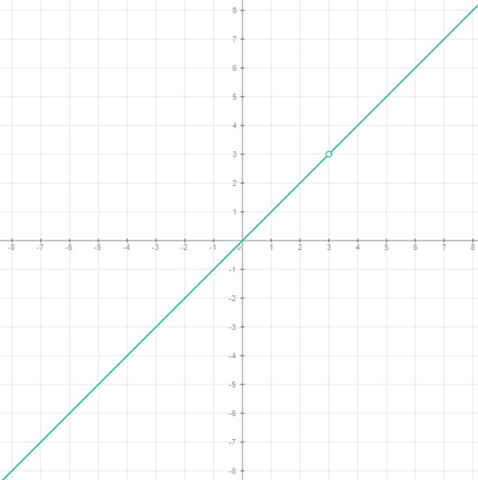
Область определения: x∈(-∞; 3)U(3; +∞)

Нули функции: x=0

Функция линейная (y=x, значение функции равно значению аргумента. биссектриса 1 и 3 координатных углов). Точка при x=3 выколота. График приложен.

По графику определяем, что значения функции отрицательны, когда аргумент отрицателен.

Ответ: x<0</strong>

СРОЧНО! Постройте график функции (** картинке) . При каких значениях аргумента значения...