Найдите площадь фигуры, ограниченной линиями y=6-x^2 и y=2

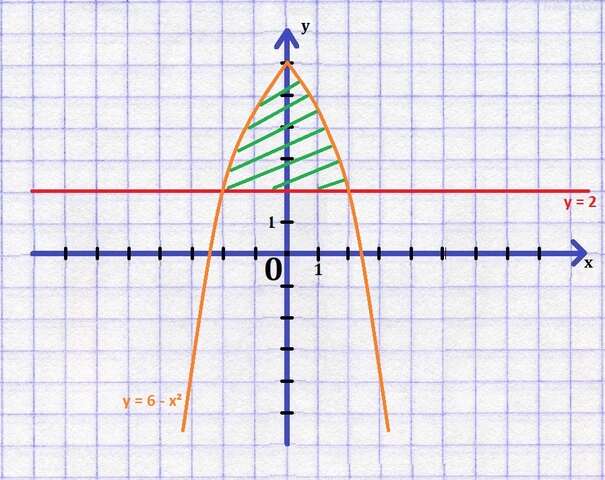
Площадь фигуры, ограниченной линиями.

Итак, найти нужно площадь криволинейной трапеции, заключённой между данными линиями.

1) Для решения таких задач, в первую очередь нужно построить график.

Расписывать построение я не буду, раз решаете задачи с интегралами, графики прямой и параболы изобразить не проблема.

График смотри в приложении.

2) По графику видно, что $x \in [-2; 2]$ , это и будут наши пределы интегрирования.

3) Если на отрезке $[-2; 2]$ непрерывная функция $y = 6 - x^2$ больше либо равна непрерывной функции $y = 2$ , то площадь фигуры, ограниченной графиками данных функций и прямыми $x = -2, x = 2$ , можно найти так: $S = \int\limits^{2}_{-2}{\big((6-x^2) - 2\big)}dx.$

4) Вычислим полученный интеграл.

$S = \int\limits^{2}_{-2}{\big((6-x^2) - 2\big)}dx = \int\limits^{2}_{-2}{(4-x^2)}dx =\\= 4\int\limits^{2}_{-2}dx - \int\limits^{2}_{-2}{x^2}dx = 4x|^{2}_{-2} - \dfrac{1}{3}x^3|^{2}_{-2} = 4\big(2 - (-2)\big) - \dfrac{1}{3}\left(2^3 - (-2)^3\right) =\\= 4*4 - \dfrac{1}{3}*16 = 16 - 5\dfrac{1}{3} = 10\dfrac{2}{3}.$

Найдите площадь фигуры, ограниченной линиями y=6-x^2 и y=2

Площадь фигуры, ограниченной линиями.

Ответ:

Ответ: $10\dfrac{2}{3}.$