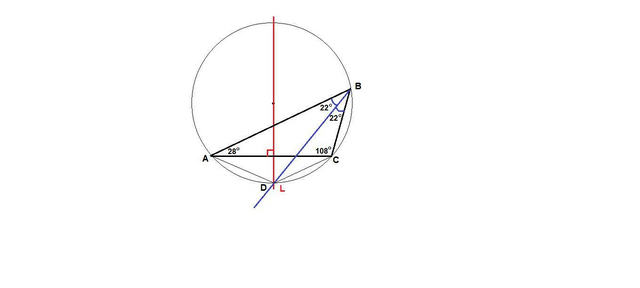
Ответ: 136°
Объяснение:
Пусть L - точка пересечения биссектрисы угла В с окружностью, описанной около треугольника АВС.
Так как вписанные углы ABL и CBL равны, то равны и дуги AL и CL, а значит равны и хорды, их стягивающие:
AL = CL.
Так как точка L равноудалена от концов отрезка АС, то она лежит на серединном перпендикуляре к отрезку АС. То есть
точка L совпадает с точкой D.
Тогда четырехугольник ABCD вписан в окружность. Значит суммы противоположных углов в нем равны 180°.
∠ADC = 180° - ∠ABC = 180° - 44° = 136°