S(бок)=AD*π*R
AD=5
π знаем, значит,осталось лишь найти радиус.
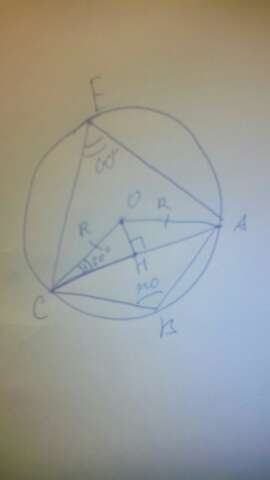
Для этого давайте рассмотрим окружность в основании. Соединим ОС и ОА. ОС=ОА=R. Треугольник СОА - р/б. Поставим точку Е на длинной дуге АС. Соединим ЕС и ЕА. Получим вписанный четырёхугольник, отсюда угол СЕА=180-АВС=60, так как угол СЕА - вписанный, при СОА - центральном, то угол СОА=2*СЕА=120 градусов. Так как СОА это р/б треугольник, то можем опустить высоту ОН. В р/б треугольнике бис=мед=выс. Отсюда СН=АС/2. Угол ОСН=180-90-120/2=30(т.к.ОН -бис, вы и медиана). Следовательно, ОС=2*ОН. ОС=СН/cos30=(3*√3)/(2*√3/2)=3, следовательно R=3.
Отсюда S(бок)=15*π
Ответ: S(бок)=15*π