Если прямая параллельна плоскости и содержится в другой плоскости, пересекающей первую, то она параллельна линии пересечения этих плоскостей.
В данном случае плоскость, которой принадлежит ∆ АВС, проходит через АВ, параллельную другой плоскости и пересекает её, поэтому линия пересечения MN этих плоскостей параллельна АВ.
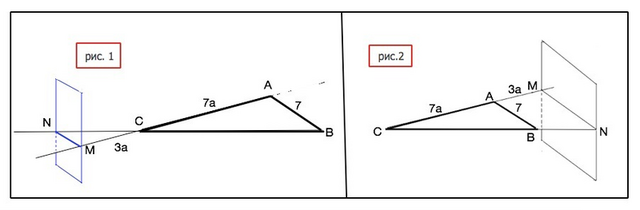
Поскольку плоскость, параллельная АВ, пересекает не сами стороны, а продолжения сторон АС и ВС, то она проходит вне треугольника. (см. рис. 1 приложения)
.Соответственные углы при пересечении параллельных прямых АВ и MN секущими АМ и ВN равны. ⇒ ∆ АВС~∆ СMN ( их углы равны). По условию MC : AC = 3 : 7, значит, ∆ MNC меньше сходственных сторон ∆ АВС, и МN пересекает плоскость, в которой лежит ∆ АВС, по другую сторону от т.С. (см. рисунок)
Примем коэффициент отношения МС:АС=а.
Тогда АС=7а, СМ=3а, а АМ=7а+3а=10 а.
Из подобия следует отношение:
СМ:АС=MN:AB
3a:7a=MN:7⇒
7 MN=21
MN=21:7=3 (ед. длины)
----------
Если MN проходит по ту же сторону от С, что АВ, то в условии ошибка и отношение МС:АС не может быть 3:7, но может быть МА:АС=3:7
Тогда МС:АС=3:7, откуда МС=10 а (см. рис. 2)⇒
MN:AB=MC:AC
MN:7=10:7⇒
MN=10 ( ед.длины)