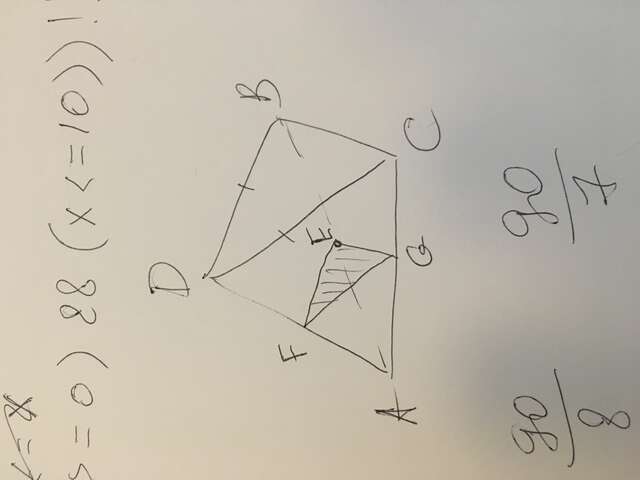Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельные прямые. Следовательно нам надо найти в плоскости ADB прямую параллельную DB и проходящую через точку E.
Следовательно это будет прямая содержащая отрезок EF - среднюю линию ΔADB.
Повторив эти рассуждения для плоскостей ABC и ADC, получим, что сечением будет ΔEFG образованный средними линиями EF, FG и GE треугольников ADB, ADC и ABC соответственно.
В каждом из треугольников мы знаем сторону основания, соответственно можем найти средние линии:
EF = FG = 7.5
FG = 9
Найдем площадь треугольника EFG, найдя высоту FH проведенную к основанию EG равнобедренного трегольника EFG

Теперь найдем и площадь сечения по формуле полупроизведения высоты на основание:
S = 6 * 9 / 2 = 27