В рівнобедреному трикутнику авс ав=ас=10 см, вс=12 см. ам - перепендикуляр до площини...

Question

В рівнобедреному трикутнику авс ав=ас=10 см, вс=12 см. ам - перепендикуляр до площини трикутника. Площина МВС утворює з площиною трикутника кут 45 градусів. Знайти: 1) АМ 2) тангенс кута нахилу прямої МС до площини трикутника 3)площу трикутника МВС

Answer 1

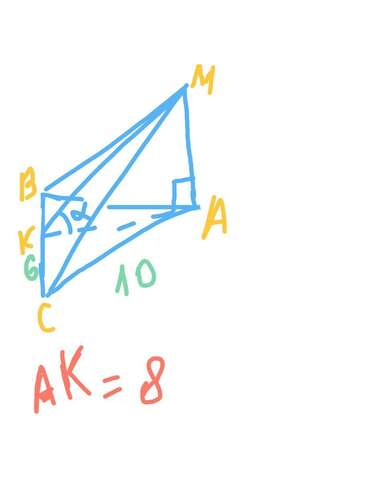
1)Розглянемо ∆АВС:
Проведемо висоту АК, за властивістю висота в рібнобедренному трикутнику, АК - висота, бісектриса , медіана
Отже КС = 12/2=6см
Розглянемо ∆АКС :
За теоремою Піфагора
АК=8см
Так як АМ - перпендикуляр до площини основи, то трикутник МАК - прямокутний
за трьома Перпендикулярами (Перпендикуляр, похила і її проекція)
За умовою задачі кут МКА=45° , а отже він так само рівнобедренний (якщо МКА 45°, то КАМ так само 45°)
Отже АМ=АК=8см.
2)Розглянемо ∆САМ:
СА = 10см за умовою задачі, АМ = 8см ,
tg кута МСА = АМ/АС = 8/10=4/5
3) З трикутника МАК знайдемо МК(за т. Піфагора)
МК= √128 = 2√32 =8√2
Розглянемо ∆ ВМС , так як він рівнобедренний, то Його площа дорівнює -

Тобто, S = 0.5 * 12 * 8√2 = 48√2 cm²

---