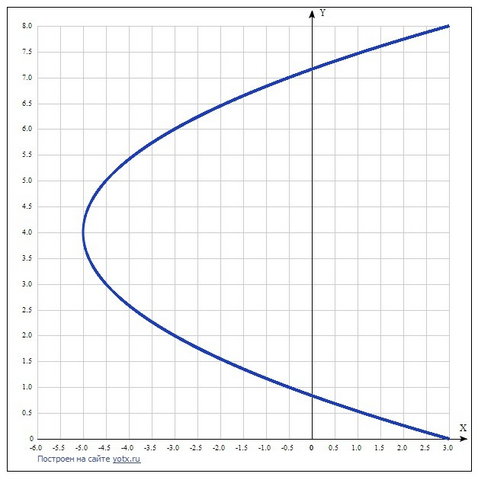
Дано уравнение кривой второго порядка y²-2x-8y+6 = 0.
Выделяем полные квадраты для y:
(y²-2*4y + 4²) - 1*4² = (y-4)² - 16.
Преобразуем исходное уравнение:
(y-4)² = 2x + 10
Получили уравнение параболы:
(y - y0)² = 2p(x - x0).
(y - 4)² = 2*1(x - (-5)).
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (-5;4)
Параметр p = 1.
Координаты фокуса: F = (x0 + (p/2)); Yo) = (-5 + (1/2)); 4) = (-4,5; 4).
Уравнение директрисы: x = x0 - p/2
x = -5 - 1/2 = -11/2.