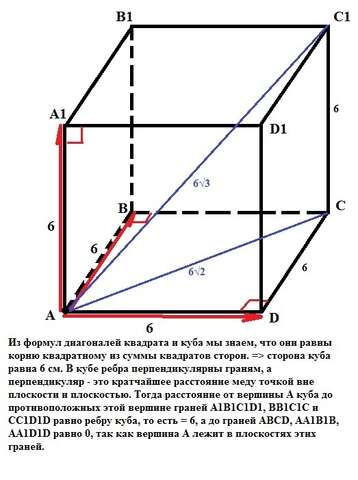
Из формул диагоналей квадрата и куба мы знаем, что они равны корню квадратному из суммы квадратов сторон. => сторона куба равна 6 см. В кубе ребра перпендикулярны граням, а перпендикуляр - это кратчайшее расстояние меду точкой вне плоскости и плоскостью. Тогда расстояние от вершины А куба до противоположных этой вершине граней А1В1С1D1, ВВ1С1С и СС1D1D равно ребру куба, то есть = 6, а до граней АВСD, AA1B1B, AA1D1D равно 0, так как вершина А лежит в плоскостях этих граней.