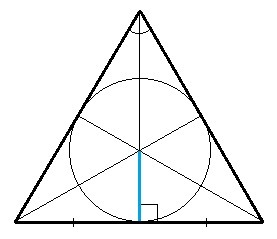
Центр окружности, вписанной в угол, лежит на биссектрисе угла. А центром окружности, вписанной в треугольник (то есть в три угла), является пересечение биссектрис углов. В равностороннем треугольнике биссектрисы являются медианами и высотами и равны между собой. Медианы треугольника точкой пересечения делятся в отношении 2:1 от вершины. Радиус вписанной окружности - перпендикуляр из центра к стороне. Таким образом, радиус вписанной окружности правильного треугольника равен 1/3 медианы.
r=15/3=5