Ответ: 3√5/5 см²
Объяснение:
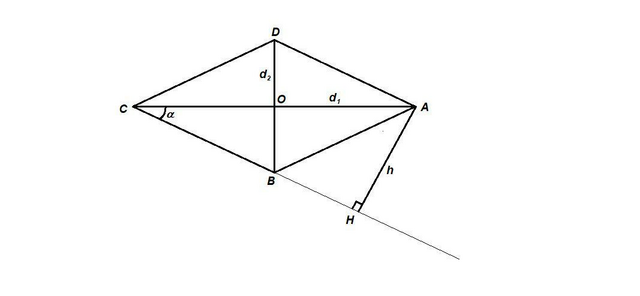
ABCD - ромб, АН = h = 4√3/6 = 2√3/3 см - высота ромба.
АС = d₁ - большая диагональ.
h = 2/3 d₁, ⇒
d₁, = 3/2 h = 3/2 · 2√3/3 = √3 см
ΔАСН: ∠АНС = 90°,
sin α = h / d₁ = 2√3/3 / √3 = 2/3
cosα = √(1 - sin²α) = √(1 - 4/9) = √(5/9) = √5/3
tg α = sinα / cosα = (2/3) : (√5/3) = 2/3 · 3/√5 = 2/√5
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
ΔОСВ: ∠СОВ = 90°, ОС = d₁/2, ОВ = d₂/2,
tg α = OB / OC
OB = OC · tgα
d₂/2 = d₁/2 · tgα = √3/2 · 2/√5 = √3/√5
d₂ = 2√3/√5
Площадь ромба:
S = 1/2 d₁ · d₂ = 1/2 · √3 · 2√3/√5 = 3/√5 = 3√5/5 см²