1) △ABC: AC=BC*tg(a) =5tg(a)
△ACD: CD=AC*sin(b) =5tg(a)*sin(b)
2) a, b - катеты, с - гипотенуза, c>a, c>b
(1) a=8 см, b=5 см, c=√(a^2+b^2) =√(64+25) =√89 (см)
(2) c=8 см, b=5 см, a=√(c^2-b^2) =√(64-25) =√39 (см)
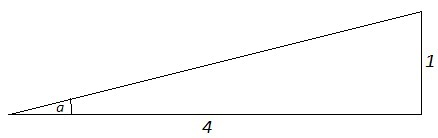
3) (a) tg a =√(1/(cos a)^2 -1) =√(17/16 -1) =1/4
(b) a - угол, противолежащий катету 1 и прилежащий катету 4 (cм. рис.)
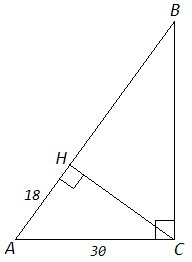
4) △ABC, AH - проекция катета AC на гипотенузу AB
AC=30 см, AH=18 см, AH/AC=3/5
△ACH - египетский треугольник (3:4:5), множ. 6.
△ABC~△ACH (по двум углам)
△ABC египетский треугольник, множ. 10 (AC=3*10).
BC=4*10=40 (см), AB=5*10=50 (см).
5) AC=4√3 м, BD=4 м
Диагонали ромба перпендикулярны, точкой пересечения делятся пополам.
△ABO - прямоугольный треугольник, AO=AC/2, BO=BD/2
ctg(BAO)= AO/BO =AC/BD =4√3/4 =√3
∠BAO=arcctg(√3) =30°, ∠ABO=90°-30°=60°
Диагонали ромба являются биссектрисами его углов. Противоположные углы ромба равны.
∠BCD=∠BAD=2∠BAO =60°
∠ADC=∠ABC=2∠ABO =120°