Если функция достигает наибольшего или наименьшего значения в точке x_0∈(a,b) и имеет в...

Question

Если функция достигает наибольшего или наименьшего значения в точке x_0∈(a,b) и имеет в этой точке производную, то:

---

Answer 1

Ответ:

f'(x) = 0

Пошаговое объяснение:

По определению: Если функция f(x) определена и дифференцируема на некотором промежутке (a,b) и во внутренней точке x₀ этого промежутка принимает наибольшее (наименьшее) значение, то необходимо, чтобы f'(x) = 0

Answer 2

ОТВЕТ: Производная равна 0.

Пошаговое объяснение:

Производная в точках локальных экстремумов равна НУЛЮ.

Физический смысл первой производной - скорость  изменения функции - она остановилась.

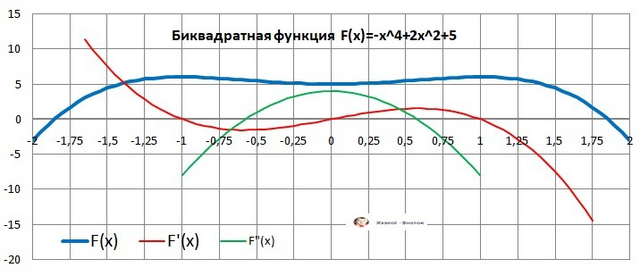
Для большего понимания на рисунке в приложении график и её производных биквадратной функции.

Посмотрите как  всё это отражается на графиках.

В корнях первой производной (красная линия) - локальные экстремума.

В корнях второй производной (зелёная линия) - точки перегиба.

Посмотрите и .... запомните на всю жизнь.

Первая производная функции движения - скорость.

Вторая производная -  ускорение.

Пригодится для решения задач по физике.

Это называется "ответ Замятина" - силой Разума.

---