Помогите даю 50 балов. Найти ВС,АD

Question

Дано ответов: 2

estern_zn · Answer 1 · 2020-05-26T14:04:12+0000

Радиус вписанной в трапецию окружности нетрудно найти - это половина ее высоты. Высоту находим как катет прямоугольного треугольника с гипотенузой BA = 18+8 и нижним катетом 18-8 = 10.

2r = h = корень(26*26-10*10)= 24

Теперь разность сторон справа NC - KC = корень(30*30-24*24) = 18

Полная разность параллельных сторон AD-BC = 18-8+18= 28

А их сумма AD+BC должна быть равна AB + CD = 56 (условие вписания окружности в трапецию).

Из первого получается AD = 28+BC

Из второго AD + BC = 28 + 2*BC = 56 или BC = 14, AD = 28+14 = 42

as11111_zn · Answer 2 · 2020-05-26T14:04:12+0000

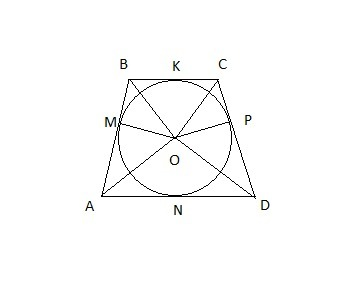
Т.к. O - центр вписанной окружности, то он лежит на биссектрисах всех углов трапеции ⇒ AO, BO, CO, DO - биссектрисы соответствующих углов трапеции.

Т.к. сумма смежных углов трапеции равна 180°, то запишем:

∠BAD + ∠ABC = 180°

∠ADC + ∠BCD = 180°

Найдем сумму углов:

∠OAB + ∠OBA = ∠BAD / 2 + ∠ABC / 2 = (∠BAD + ∠ABC) / 2 = 180° / 2 = 90°

Следовательно ∠AOB = 90° (т.к. сумма углов ΔAOB = 180°)

Аналогично докажем, что ∠COD= 90°

В прямоугольных треугольниках AOB и COD для высот проведенных к гипотенузе имеем соотношения:

$OM^2=AM*BM\\OP^2=DP*CP$

Но OM = OP как радиусы вписанной окружности ⇒ AM*BM = DP*CP ⇒ DP * CP = 8 * 18 = 144

Кроме того, DP + CP = CD = 30

Решаем систему уравнений:

$\left\{{{DP*CP=144}\atop{DP+CP=30}}\right.$

По теореме Виета (с учетом того, что CP < DP) CP = 6, DP = 24

Из условия равенства касательных проведенных из одной точки к окружности выпишем следующие равенства:

BK = BM, CK = CP, DP = DN, AM = AN

Теперь можем вычислить основания трапеции:

AD = AN + DN = AM + DP = 18 + 24 = 42

BC = BK + CK = BM + CP = 8 + 6 = 14