Интересная задача! Много баллов!

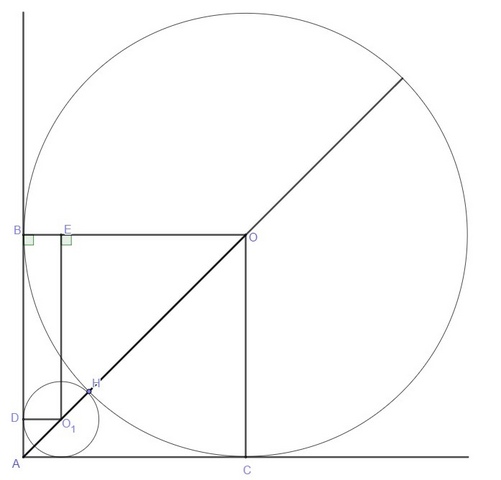
Задача. В прямой угол вписана окружность с радиусом (3+2√2). Найти радиус меньшей окружности, также вписанной в этот угол и касающейся данной окружности.

Решение:

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности

AB = AC и АО - биссектриса угла ВАС, значит ΔАОВ - равнобедренный прямоугольный треугольник из этого следует, что AB = OB; тогда OA = OB√2 = (3+2√2)√2 = 4 + 3√2

Проведем O₁E ⊥ OB и обозначим O₁H = x - искомый радиус, тогда

$OO_1=x+3+2\sqrt{2}\\ EO=3+2\sqrt{2}-x$

Из подобия треугольников АОВ и $O_1EO$ :

AO/OO₁ = OB/OE ⇒ $\dfrac{4+3\sqrt{2}}{x+3+2\sqrt{2}}=\dfrac{3+2\sqrt{2}}{3+2\sqrt{2}-x}$

$(4+3\sqrt{2})(3+2\sqrt{2}-x)=(3+2\sqrt{2})(x+3+2\sqrt{2})\\ 12+8\sqrt{2}-4x+9\sqrt{2}+12-3x\sqrt{2}=3x+9+6\sqrt{2}+2x\sqrt{2}+6\sqrt{2}+8\\ 5\sqrt{2}+7=5x\sqrt{2}+7x\\ 5\sqrt{2}+7=(5\sqrt{2}+7)x\\ x=1$

Ответ: 1 см.