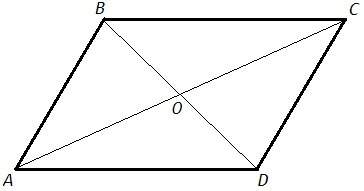
Противоположные стороны параллелограмма равны.
AB=CD, BC=AD
Диагонали параллелограмма точкой пересечения делятся пополам.
AO=CO, BO=DO
Диагонали делят параллелограмм на две пары равных треугольников.
△AOB=△COD, △BOC=△DOA (по трем сторонам)
Рассмотрим неравные треугольники AOB и BOC, пусть BC>AB
P(BOC)-P(AOB)= BO+CO+BC-AO-BO-AB =BC-AB =2
P(ABCD)= AB+BC+CD+AD =2(BC+AB) =44 <=> BC+AB =22
Сложим полученные равенства
2BC=24 <=> BC=12