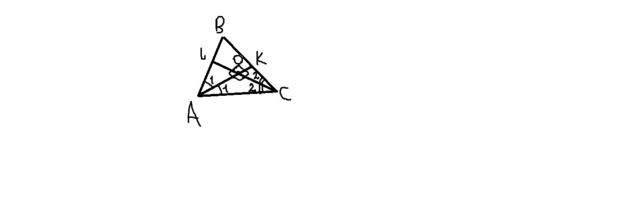
1). Предположим, что такой треугольник и в правду существует. Пусть есть некий треугольник ABC, в котором проведены биссектрисы AK и CL. Для удобства обозначим ∠KAC=∠KAB=∠1, а ∠LCA=∠LCB=∠2 (эти углы равны, т.к. AK и CL - биссектрисы). Биссектрисы AK и CL перпендикулярны и пересекаются в точке О, т.е. ∠AOL=90°, тогда ∠AOC=180°-∠AOL=90°, как смежный. ∠LOK=∠AOC=90°, как вертикальные. ∠COK=∠AOL=90°, как вертикальные. Получаем, что ∠AOL=∠AOC=∠LOK=∠COK=90°;
2). Рассмотрим прямоугольный треугольник AOC, т.к. ∠AOC=90°. В треугольнике AOC ∠1+∠2=90°, как сумма острых углов в прямоугольном треугольнике (∠1=∠KAC, ∠2=∠LCA из предыдудшего пункта);
3). Рассмотрим прямоугольный треугольник AOL, т.к. ∠AOL=90°. ∠1+∠ALO=90°, как сумма острых углов прямоугольного треугольника AOL. Тогда ∠ALO=90°-∠1;
4). Рассмотрим прямоугольный треугольник COK, т.к. ∠COK=90°. ∠2+∠CKO=90°, как сумма острых углов прямоугольного треугольника COK. Тогда ∠CKO=90°-∠2;
5). Рассмотрим четырехугольник LBKO:
∠BLO=180°-∠ALO, как смежный угол. Подставив значение ∠ALO из п. 3, получаем:
∠BLO=180°-90°+∠1=90°+∠1;
Аналогично ∠BKO=180°-∠CKO, как смежный угол. Подставив значение ∠CKO из п. 4, получаем:
∠BKO=180°-90°+∠2=90°+∠2;
∠LOK=90° из п. 1;
Т.к. сумма всех углов четырехугольника равна 360°, то:
∠BLO+∠BKO+∠LOK+∠LBK=360°;
Подставив найденные значения, получаем:
90°+∠1+90°+∠2+90°+∠LBK=360°;
270°+∠1+∠2+∠LBK=360°;
∠1+∠2=90°-∠LBK;
6). Но в п. 2 мы выяснили, что ∠1+∠2=90°, получается некоторое противоречие:
∠1+∠2=90°
∠1+∠2=90°-∠LBK
Такого быть не может, а значит треугольника, в котором две биссектрисы взаимно перпендикулярны, не существует.
Ответ: Нет, не существует.