** диагонали BD квадрата ABCD отметили точку E так, что DE=AD . Через точку E проведена...

Question

На диагонали BD квадрата ABCD отметили точку E так, что DE=AD . Через точку E проведена прямая , которая перепендикулярна прямой BD и пересекает сторону AB в точке F. Докажите что AF=FE=BE

Answer 1

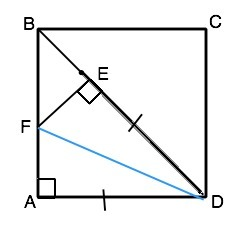
   Диагонали квадрата делят его углы пополам. Угол АВD=90°:2=45° ⇒ Угол FBE=180°-90°-45°=45°, поэтому треугольник ВЕF - равнобедренный, ВЕ=FЕ. Соединим точки F и D и получим прямоугольные ∆ АFD и ∆ DFE. Эти треугольники равны по катету ( ED=AD по условию) и общей гипотенузе FD. ⇒ EF=AF, а так как EF=BE, то  AF=FE=BE

---