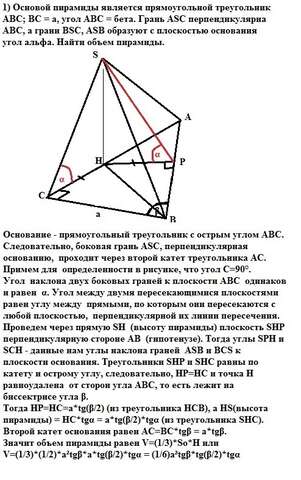
1) Основание - прямоугольный треугольник с острым углом АВС. Следовательно, боковая грань АSC, перпендикулярная основанию, проходит через второй катет треугольника АС. Примем для определенности в рисунке, что угол С=90°.
Угол наклона двух боковых граней к плоскости АВС одинаков и равен α. Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. Проведем через прямую SН (высоту пирамиды) плоскость SHP перпендикулярную стороне АВ (гипотенузе). Тогда углы SPH и SСH - данные нам углы наклона граней АSВ и ВCS к плоскости основания. Треугольники SHP и SHС равны по катету и острому углу, следовательно, НР=НС и точка Н равноудалена от сторон угла АВС, то есть лежит на биссектрисе угла β.
Тогда НР=НС=a*tg(β/2) (из треугольника НСВ), а
НS(высота пирамиды) = HC*tgα = a*tg(β/2)*tgα (из треугольника SHC). Второй катет основания равен АС=ВС*tgβ = a*tgβ.
Значит объем пирамиды равен V=(1/3)*So*H или
V=(1/3)*(1/2)*a²tgβ*a*tg(β/2)*tgα = (1/6)a³tgβ*tg(β/2)*tgα.
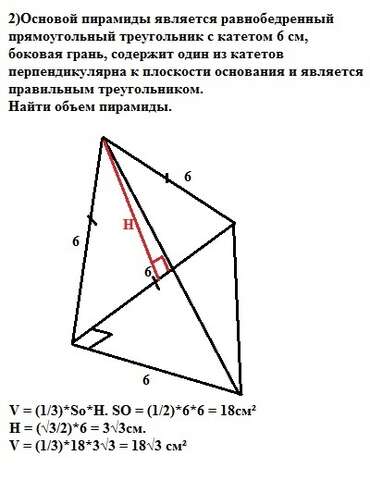
2) Объем пирамиды V = (1/3)*So*H. (формула). Основание - прямоугольный треугольник и его площадь равна половине произведения катетов. Sо = (1/2)*6*6 = 18см²
Боковая грань, перпендикулярная основанию - правильный треугольник и его высота является и высотой пирамиды. Нахлдим эту высоту по формуле:
Н = (√3/2)*6 = 3√3см. Тогда объем нашей пирамиды равен
V = (1/3)*18*3√3 = 18√3 см².