Дано: Y = (x³ - 5x² + 6x)/x - функция.
Исследование, график.
Пошаговое объяснение:
1. Область определения - D(y) - X≠0, X∈(-∞;0)∪(0;+∞) - разрыв при Х=0.
2. Поведение в точке разрыва.
lim(->0-) Y(x) = 6, lim(->0+) = 6 . Пределы равны - разрыв 1-го рода.
Далее упрощаем функцию и получаем обычную параболу:
Y(x) = x² - 5*x +6.
3. Нули функции: Y(x)= (x-3)*(x-2) = 0
x1 = 2, x2 = 3.
4. Функция ни чётная, ни нечётная.
5. Первая производная: Y'(x) = 2x + 5 = 0.
Корень производной. Х = 2,5 - точка экстремума.
6. Локальный экстремум - Ymin(2.5) = - 1/4 = - 0.25.
7. Интервалы монотонности.
Убывает: X∈(-∞;2.5]. Возрастает: Х∈[2.5;+∞) - здесь функция непрерывная - квадратные скобки.
8. Вторая производная: Y"(x) = 2 > 0.
9. Вогнутая - "ложка" - Х∈(-∞;0)∪(0;+∞) - везде где существует.
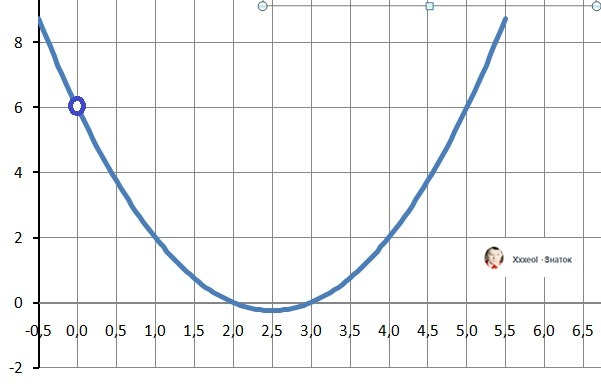
10. График функции на рисунке в приложении.
Разрыв на графике отмечается "дыркой" - кольцом.