Биссектриса внешнего угла A пересекает прямую, содержащую среднюю линию треугольника ABC,...

Question

Биссектриса внешнего угла A пересекает прямую, содержащую среднюю линию треугольника ABC, параллельную стороне AB, в точке X. Найдите ∠XCA, если ∠CAB=54 ∘ .

Answer 1

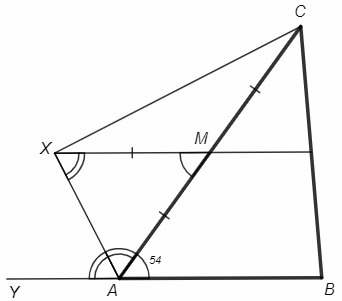
∠YAC - внешний угол, M - середина AC

∠YAX=∠MAX (AX - биссектриса ∠YAC)

∠YAX=∠MXA (накрест лежащие при XM||AB)

∠MAX=∠MXA => △XMA - равнобедренный, XM=MA

XM=MC, △XMC - равнобедренный => ∠XCA=∠MXC

∠XMA=2∠XCA (внешний угол равен сумме внутренних, не смежных с ним)

∠XMA=∠CAB=54 (накрест лежащие при XM||AB)

∠XCA=∠XMA/2 =54/2 =27

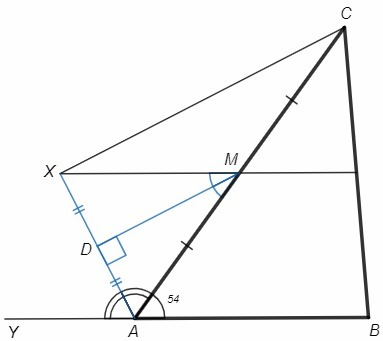
Или  проведем биссектрису MD угла XMA. Биссектрисы внутренних углов при параллельных перпендикулярны, MD⊥AX. Биссектриса MD является высотой, следовательно и медианой. MD - средняя линия в треугольнике CAX, MD||CX. ∠XCA=∠DMA как соответственные. ∠XMA=∠CAB как накрест лежащие при XM||AB. ∠XCA=∠XMA/2=∠CAB/2=27

---

---

Comments

Сумма внутренних углов при параллельных 180, сумма их половин 90. В треугольнике, образованном биссектрисами, сумма двух углов 90, следовательно третий - прямой, биссектрисы перпендикулярны.

---

спасибо за полный и понятный ответ.

---

То, что биссектриса угла при параллельных отсекает равнобедренный треугольник, часто используется в задачах. Биссектриса угла параллелограмма, биссектриса угла трапеции отсекают равнобедренный треугольник.