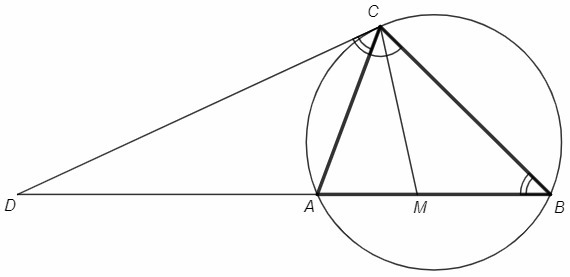
∠ACD =∪AC/2 =∠ABC (угол между касательной и хордой)
△ACD~△CBD (по двум углам, ∠D - общий)
AC/CB =CD/BD =AD/CD
AC/CB =AM/MB =9/12 =3/4 (по теореме о биссектрисе)
BD=4/3 CD, AD=3/4 CD
BD-AD=AB => 4/3 CD -3/4 CD =21 <=> CD=21*12/7 =36
Или
∠ACD =∪AC/2 =∠B =>
∠DCM =∠ACD+∠C/2 =∠B+∠C/2 =∠DMC
△CDM - равнобедренный, DC=DM
Квадрат касательной равен произведению секущей на ее внешнюю часть.
DC^2 =DB*DA
DA=DM-AM, DB=DM+MB
DC^2 =(DC+MB)(DC-AM) <=>
DC^2 =DC^2 +MB*DC -AM*DC -AM*MB <=>
DC=AM*MB/(MB-AM) =9*12/(12-9) =36