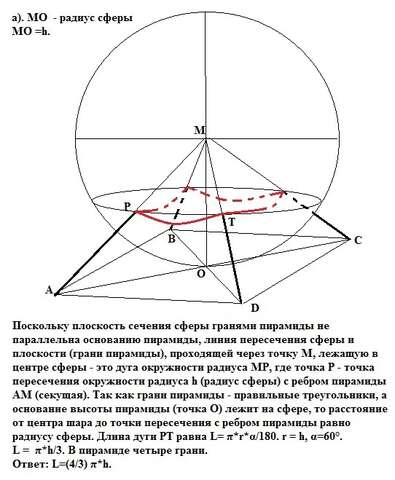
а). МО - радиус сферы МО =h.
Поскольку плоскость сечения сферы гранями пирамиды не параллельна основанию пирамиды, линия пересечения сферы и плоскости (грани пирамиды), проходящей через точку М, лежащую в центре сферы - это дуга окружности радиуса МР, где точка Р - точка пересечения окружности радиуса h (радиус сферы) с ребром пирамиды АМ (секущая). Так как грани пирамиды - правильные треугольники, а основание высоты пирамиды (точка О) лежит на сфере, то расстояние от центра сферы до точки Р пересечения с ребром пирамиды равно радиусу сферы. Длина дуги РТ равна L= π*r*α/180. r = h, α=60°.
L = π*h/3. В пирамиде четыре грани.
Ответ: L=(4/3) π*h.
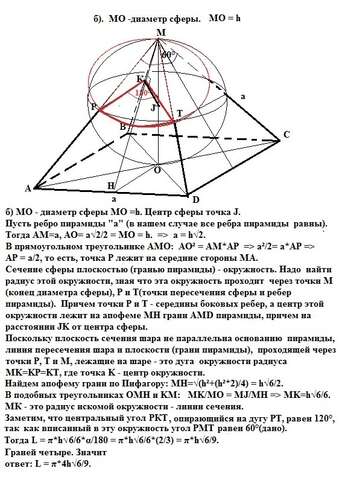
б) МО - диаметр сферы МО =h. Центр сферы точка J.
Пусть ребро пирамиды "а" (в нашем случае все ребра пирамиды равны). Тогда АМ=а, АО= а√2/2 = MO = h. =>
а = h√2.
В прямоугольном треугольнике АМО: АО² = АМ*АР => а²/2= a*AP => АР = а/2, то есть, точка Р лежит на середине стороны МА. Сечение сферы плоскостью (гранью пирамиды) - окружность. Надо найти радиус этой окружности, зная что эта окружность проходит через точки М(конец диаметра сферы), Р и Т(точки пересечения сферы и ребер пирамиды). Причем точки Р и Т - середины боковых ребер, а центр этой окружности лежит на апофеме МН грани AMD пирамиды, причем на расстоянии JK от центра сферы.
Поскольку плоскость сечения шара не параллельна основанию пирамиды, линия пересечения шара и плоскости (грани пирамиды), проходящей через точки Р, Т и М, лежащие на шаре - это дуга окружности радиуса МK=KP=KT, где точка K - центр окружности.
Найдем апофему грани по Пифагору: МН=√(h²+(h²*2)/4) = h√6/2. В подобных треугольниках ОМН и KMJ отношение MK/MO = MJ/MH => MK=h√6/6.
МК - это радиус искомой окружности - линии сечения.
Заметим, что центральный угол РКТ, опирающийся на дугу РТ, равен 120°, так как вписанный в эту окружность угол РМТ равен 60°(дано).
Тогда L = π*h√6/6*α/180 = π*h√6/6*(2/3) = π*h√6/9.
Граней четыре. Значит
ответ: L = π*4h√6/9.