|x|≥0 по определению.
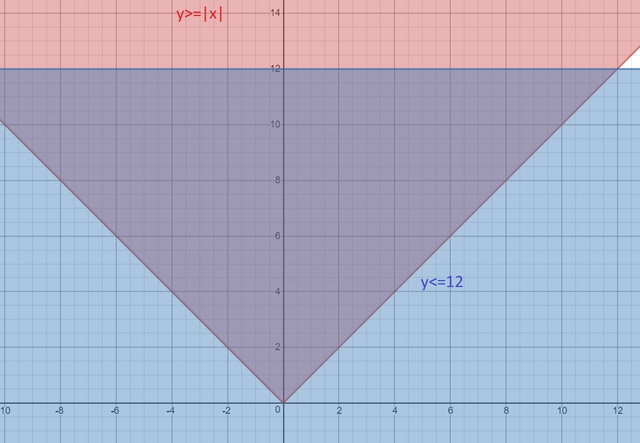
|x|≤y; y не может быть меньше нуля т.к. модуль не может быть меньше нуля, минимальное значение х это 0. Значит y≥0. Безусловно можно рассматривать и при других значениях X, но все последующие значения Y будут объединены вместе как одно, и при этом Y всегда будет больше какого-то числа, которое ≥ 0. А потом всё это просто пересекается со вторым утверждение y≤0. Выглядит это так:
![\left \{ {{y\leq 12} \atop {\left[\begin{array}{ccc}y\geq 0\\y\geq 1\\y\geq 2/3\\y\geq 10\\y\geq 143\\_:^:\end{array}\right] }}](https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7By%5Cleq%2012%7D%20%5Catop%20%7B%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Dy%5Cgeq%200%5C%5Cy%5Cgeq%201%5C%5Cy%5Cgeq%202%2F3%5C%5Cy%5Cgeq%2010%5C%5Cy%5Cgeq%20143%5C%5C_%3A%5E%3A%5Cend%7Barray%7D%5Cright%5D%20%7D%7D "\left \{ {{y\leq 12} \atop {\left[\begin{array}{ccc}y\geq 0\\y\geq 1\\y\geq 2/3\\y\geq 10\\y\geq 143\\_:^:\end{array}\right] }}")
В итоге получается 0≤y≤12
Ответ: y∈[0;12]
Так же смотри наглядный график.
