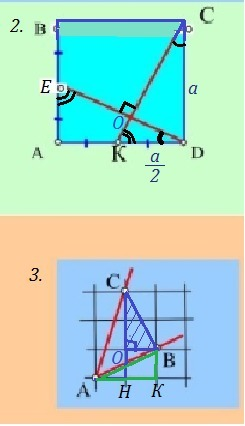
2) Рассмотрим ΔАДЕ, ∠А=90° , АД=а , АЕ=а/2 ⇒ ∠АДЕ лежит напротив катета АЕ, равного половине гипотенузы ДЕ ⇒ ∠АДЕ=30°.
Рассм. ΔСДК , ∠Д=90° , ∠КСД=30°, как угол, лежащий напротив катета КД, равного половине гипотенузы КС ( СД=а , КД=а/2 ). Тогда ∠ДКС=180°-90°-30°=60°
Рассм. ΔКОД , ∠АДЕ=30° , ∠ДКС=60° , ∠КОД=180°-30°-60°=90° ⇒
ОК⊥ДО ⇒ СК⊥ДЕ , ч.т.д.
3) Построим ΔСОВ ( см. на рис.), ∠О=90° ⇒
СВ=√(ОС²+ОВ²)=√(2²+1²)=√5 , СВ²=(√5)²=5 .
ΔАСН , ∠АНС=90° , АС=√(АН²+СН²)=√(1²+3²)=√10 .
ΔАВК , ∠АКВ=90° , АВ=√(АК²+ВК²)=√(2²+1²)=√5 .
АС²-АВ²=(√10)²-(√5)²=10-5=5=ВС² ⇒ АС²=АВ²+ВС² ⇒ выполнены условия теоремы Пифагора ⇒ ∠АВС=90° , ВС=АВ=√5 ⇒ ΔАВС - равнобедренный прямоугольный треугольник ⇒ ∠ВАС=∠АСВ=45° .