ПОМОГИТЕ!!! Отрезок AB и CD - диаметры окружности с центром в точке О. Хорда BD = 15см, а...

Question

ПОМОГИТЕ!!! Отрезок AB и CD - диаметры окружности с центром в точке О. Хорда BD = 15см, а радиус окружности 9 см. Доказать, что AOC и DOB равны. Вычислить периметр треугольника AOC. ( Сделать все правильно и четко, с решением и с рисунком, желательно сделать на листочке, если сложно напишите хотя-бы доказательство, но желательно найти еще и периметр).

Answer 1

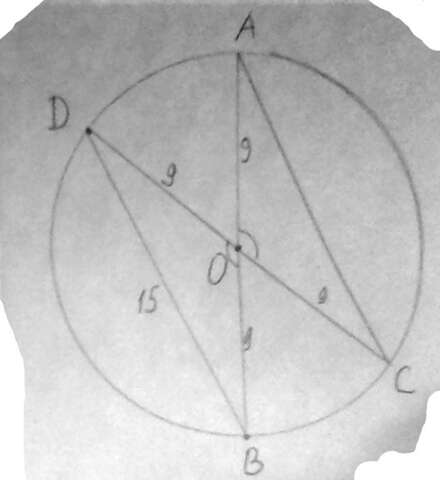
ΔАОС = ΔDOB по первому признаку равенства треугольников (две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треуольника)

Докажем это.

ΔАОС образован отрезками ОА и ОС, равными радиусу окружности, и отрезком АС.

ΔDOB образован отрезками ОD и ОВ, равными радиусу окружности, и отрезком АС.

∠ВОD=∠АОС, т.к. развернутый ∠АОВ=180=∠ВОD+∠DОА и развернутый ∠DОС=180=∠DОА+∠АОС, откуда следует, что ∠ВОD+∠DОА=∠DОА+∠АОС ⇒ ∠ВОD=∠АОС.

Итого имеем две равных стороны и угол между ними. Треугольники ΔАОС и ΔDOB  равны.

Из равенства треугольников следует, что все стороны у них равны, поэтому BD=AC=15 см.

Периметр ΔАОС=АО+ОС+АС=9+9+15=33 см

---