Решите пожалуйста второе задание.

Question

Дан 1 ответ

Правильный ответ

$f(x)=-x^2+2x+3\\ a=-1, b=2, c=3;$

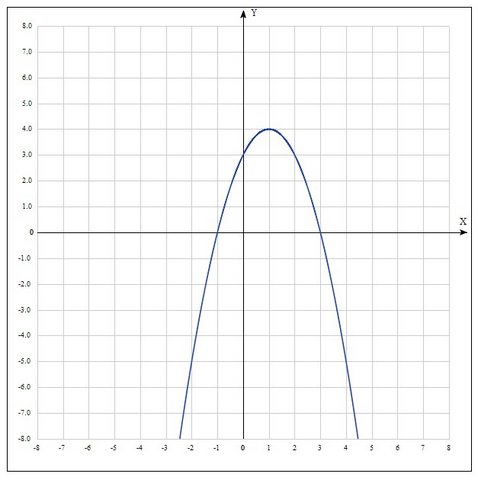
Квадратичная функция, график - парабола.

Так как $a<0$ , ветви направлены вниз.

Построение:

Шаг 1. Ищем вершину графика.

$x_{0}=-\frac{b}{2a}=-\frac{2}{2*(-1)}=1,\\ y_{0}=-1^2+2*1+3=4$

Шаг 2. Строим график $f(x)=-x^2+2x+3$ по точкам, от вершины.

$f(-2)=-(-2)^2+2*(-2)+3=-5,\\ f(-1)=-(-1)^2+2*(-1)+3=0,\\ f(0)=-0^2+2*0+3=3,\\ f(1)=-1^2+2*1+3=4,\\ f(2)=-2^2+2*2+3=3$

Анализируя график, легко увидеть, что функция убывает на промежутке $[1;+\infty)$ , а возрастает на промежутке $(-\infty; 1]$ .

Можно сделать и "вслепую" - взять производную.

$f'(x)=(-x^2+2x+3)'=-2x+2\\ ]-2x+2=0,\\ -2x=-2,\\ x=1$

$f(1)=4$ - максимум (наибольшее значение) функции.

Минимумы у данной функции отсутствуют.

При каких значениях $x$ функция отрицательна?

Анализируя график, легко увидеть, что функция отрицательна на промежутках $(-\infty; -1);(3;+\infty)$

Если же решать "вслепую", то:

При $x$ , являющихся решением неравенства $-x^2+2x+3<0$

0\\ ]x^2-2x-3=0,\\ a=1,b=-2,c=-3;\\ D=b^2-4ac=(-2)^2-4*1*(-3)=4+12=16,>0;\\ x_{1,2} =\frac{-b \pm \sqrt{D} }{2a}=\frac{2 \pm \sqrt{16} }{2*1}=\left \ [ {{3} \atop {-1}} \right." alt="-x^2+2x+3<0, |*(-1)\\ x^2-2x-3>0\\ ]x^2-2x-3=0,\\ a=1,b=-2,c=-3;\\ D=b^2-4ac=(-2)^2-4*1*(-3)=4+12=16,>0;\\ x_{1,2} =\frac{-b \pm \sqrt{D} }{2a}=\frac{2 \pm \sqrt{16} }{2*1}=\left \ [ {{3} \atop {-1}} \right." align="absmiddle" class="latex-formula">

Разложим данный двучлен на множители.

$a(x-x_{1})(x-x_{2})=(x-3)(x+1)$

Помним, что мы решаем неравенство: 0" alt="(x-3)(x+1)>0" align="absmiddle" class="latex-formula">

Начертим $Ox$ , отметим на ней точки $\{3\}$ и $\{1\}$ .

Имеем три промежутка: $(-\infty;-1);(-1;3);(3;+\infty)$ , причём точки $\{3\}$ и $\{1\}$ не включены, так как неравенство строгое.

Подставим любое число, большее $\{3\}$ и $\{1\}$ , в неравенство 0" alt="(x-3)(x+1)>0" align="absmiddle" class="latex-formula">. Пусть $x=1000$ , тогда $(1000-3)(100+1)$ , больше $0$ . Данный промежуток нам подходит. Далее, очевидно, промежуток $(-1;3)$ даёт решения меньше $0$ , а $(-\infty;-1)$ - решения больше нуля, данный промежуток нам тоже подходит.

Итак, решение неравенства: $x \in (-\infty; -1) \cup (3;+\infty)$

Murрhу_zn (4.0k баллов) 28 Май, 20