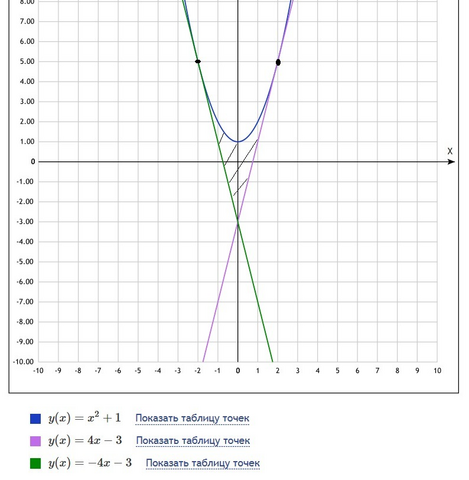
найду уравнение касательной
если касательная касается параболы в точке х=а, то ее уравнение будет
g(x)=y(a)+y`(a)(x-a)
y(a)=a^2+1
y`(a)=2a
g(x)=a^2+1+2a(x-a)
эта касательная проходит через точку (0;-3)
-3=a^2+1+2a(0-a); -3=a^2+1-2a^2=1-a^2; a^2=4; a=+-2
тогда уравнение касательной
g(x)=4x-3 и g(x)=-4x-3
учитывая симметричность фигуры, найду ее площадь как удвоенный интеграл разности функций x^2+1 и 4x-3 на интервале по х от 0 до 2
S=2∫(x^2+1-4x+3)dx=2∫(x^2-4x+4)dx=2*(x^3/3-2x^2+4x)=
подстановка пределов по х от 0 до 2
=2(8/3-8+8)=16/3=5 1/3