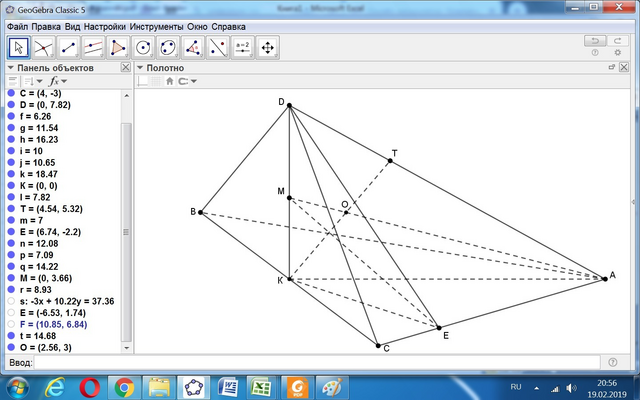
Так как в основании равнобедренный треугольник, то центр вписанного шара лежит в плоскости, проходящей через ребро АД перпендикулярно к основанию.
Центр шара находится на пересечении двух прямых:
- прямой КТ, проходящей под углом 45 градусов к плоскости основания через точку К (это середина ВС) перпендикулярно ВС,
- прямой АМ, где точка М – точка пересечения биссекториальной плоскости между плоскостями: основания и АСД с высотой пирамиды, лежащей в плоскости, проходящей через ребро АД перпендикулярно к основанию.
Точку М находим так: из точки Д опускаем перпендикуляр ДЕ на ребро АС и проводим биссектрису угла ДЕК. Отрезок АК как высота основания равен:
АК = √(502 – (60/2)2) = √(2500 – 900) = √1600 = 40.
Высота КЕ из прямого угла равна: КЕ = (30*40)/50 = 24.
Отрезок ДЕ = √(72 + 242) = √(49 + 576) = √625 = 25.
Величину КМ определяем из свойства биссектрисы и высоты пирамиды, равной 7.
КМ/24 = (7 – КМ)/25. Отсюда КМ = 168/49.
Координаты точки пересечения прямых КТ и АМ определяем в плоскости АКД.
Уравнение КТ: z = y, уравнение АМ: z = ((-168/49)/40)y + (168/49).
Приравняв их, получаем: у = (168*49*40)/(49(49*40+168) = 3,1579 ≈ 3,16.
Это и есть величина радиуса шара, вписанного в пирамиду.