0\\\\t=log+2(sinx)\; \; ,\; \; 2t^2+3-2\geq 0\; ,\; \; t_1=-2\; ,\; t_2=\frac{1}{2}\\\\2(t+2)(t-\frac{1}{2})\geq 0\; \; ,\; \; \; +++[-2\, ]---[\frac{1}{2}\, ]+++\\\\t\in (-\infty ,-2\, ]\cup [\, \frac{1}{2},+\infty )\\\\\left [ {{log_2(sinx)\leq -2} \atop {log_2(sinx)\geq \frac{1}{2}}} \right. \; \left [ {{sinx\leq 2^{-2}} \atop {sinx\geq \sqrt2}} \right. \; \left [ {{sinx\leq \frac{1}{4}} \atop {x\in \varnothing }} \right. \; \; \to\; \; \; 00\\\\t=log+2(sinx)\; \; ,\; \; 2t^2+3-2\geq 0\; ,\; \; t_1=-2\; ,\; t_2=\frac{1}{2}\\\\2(t+2)(t-\frac{1}{2})\geq 0\; \; ,\; \; \; +++[-2\, ]---[\frac{1}{2}\, ]+++\\\\t\in (-\infty ,-2\, ]\cup [\, \frac{1}{2},+\infty )\\\\\left [ {{log_2(sinx)\leq -2} \atop {log_2(sinx)\geq \frac{1}{2}}} \right. \; \left [ {{sinx\leq 2^{-2}} \atop {sinx\geq \sqrt2}} \right. \; \left [ {{sinx\leq \frac{1}{4}} \atop {x\in \varnothing }} \right. \; \; \to\; \; \; 0
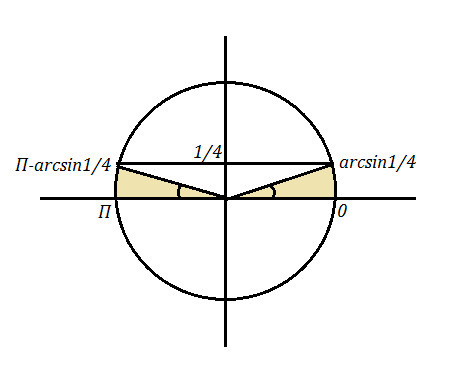
![x\in (2\pi n\, ;\, arcsin\frac{1}{4}+2\pi n\, ]\cup [\, \pi -arcsin\frac{1}{4}+2\pi n\, ;\, \pi +2\pi n\, )](https://tex.z-dn.net/?f=x%5Cin%20%282%5Cpi%20n%5C%2C%20%3B%5C%2C%20arcsin%5Cfrac%7B1%7D%7B4%7D%2B2%5Cpi%20n%5C%2C%20%5D%5Ccup%20%5B%5C%2C%20%5Cpi%20-arcsin%5Cfrac%7B1%7D%7B4%7D%2B2%5Cpi%20n%5C%2C%20%3B%5C%2C%20%5Cpi%20%2B2%5Cpi%20n%5C%2C%20%29 "x\in (2\pi n\, ;\, arcsin\frac{1}{4}+2\pi n\, ]\cup [\, \pi -arcsin\frac{1}{4}+2\pi n\, ;\, \pi +2\pi n\, )")
