Дана функция f(x)=-x^2-2x+3. 1) Запишите координаты вершины параболы. 2) Найдите ось...

Question

Дана функция f(x)=-x^2-2x+3. 1) Запишите координаты вершины параболы. 2) Найдите ось симметрии параболы. 3) Определите точки пересечения графика с осями координат. 4) Постройте график функции. 5) Найдите промежуток, в котором y>0.

Answer 1

1) Хв= -1 Ув=4

2) -1

3) (0;3); (1;0); (-3;0)

5) (-3;1)

Answer 2

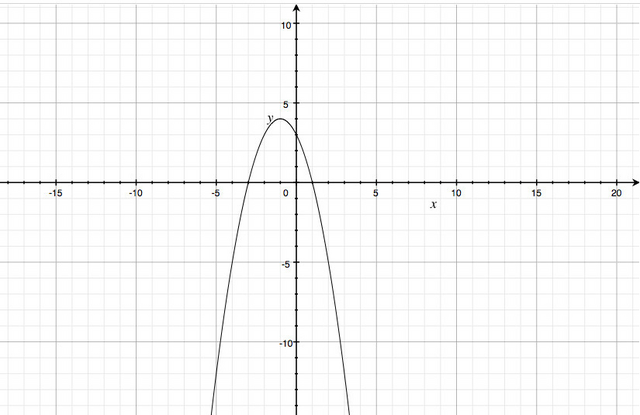
1) х вершины = -b / 2a; х = 2 / -2 = -1.

у вершины = -1 + 2 + 3 = 4.

--------------------------------------

Хв = -1

Ув = 4

2) Ось симметрии параболы проходит через вершину. С этого график оси симметрии: x = -1.

--------------------------------------

х = -1

3) Точки пересечения с осью Х - корни квадратного уравнения. С этого они ровни:

-x^2 - 2x + 3 = 0,

x^2 + 2x - 3 = 0.

За теоремой Виета: x1 = -3; x2 = 1.

Точки пересечения с осью У узнаю подставляя вместо х 0.

0 - 0 + 3 = 3.

--------------------------------------

( 0, 3 ), ( -3, 0 ), ( 1, 0 )

4) График в фото

5) -x^2 - 2x + 3 > 0;

Используя график видим, что функция больше 0 при х є ( -3 ; 1 ).

--------------------------------------

х є ( -3 ; 1 )

---