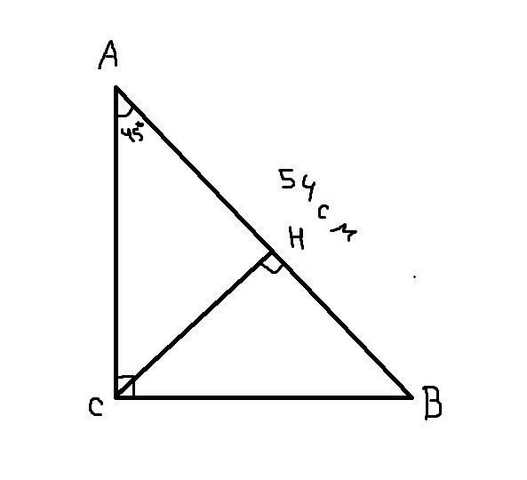
Решение:
Найдём ∠АСН:
∠АСН=180° - ∠АНС - ∠САН=180° - 90° - 45°=45°
Поскольку ∠АСН=∠САН, то ΔСАН - равнобедренный и АН=СН
Найдём ∠ВСН и ∠В:
∠В=180° - ∠С - ∠А=180° - 90° - 45°=45°
∠ВСН=180° - ∠СНВ - ∠НВС=180° - 90° - 45°=45°
Поскольку ∠ВСН=∠НВС, то ΔСВН - равнобедренный и ВН=СН
Следовательно, ВН=АН=СН
Найдём высоту СН:
АВ=АН+ВН=2ВН=54 см
ВН=27 см
СН=ВН=27 см
Ответ: 27 см