1а)
Для любого треугольника справедливо неравенство треугольника.
Каждая сторона треугольника меньше суммы двух других.
Так как 25=10+15
Неравенство треугольника не выполняется.
Треугольник со сторонами 10;15 и 25 не существует
1б)
Пусть k - коэффициент пропорциональности (k>0)
Значит, стороны треугольника
3k;5k;10k
10k<3k+5k - неверно.</p>
Неравенство треугольника не выполняется.
Треугольник со сторонами пропорциональными числам 3;5;10 не существует
в) сумма углов треугольника равна 180 градусов.
46°+64°+80°=180° - неверно, 190°≠ 180°
Треугольник с углами 46°; 64°; 80°не существует
г) Пусть k - коэффициент пропорциональности (k>0)
Значит, углы треугольника
3k ;5k ;10k
3k+5k+10k=180°
18k=180°
k=10°
Треугольник с углами 30°;50°и 100° существует.
30°:50°: 100°=3:5:10
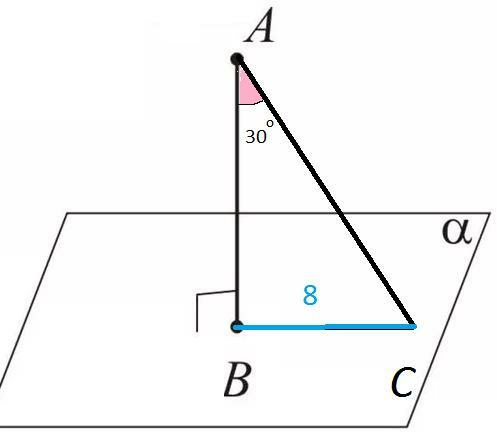
Задача 2.
В прямоугольном треугольнике против угла в 30° лежит катет, равны й половине гипотенузы.
АС=2ВС=16 см
см. рисунок