а).
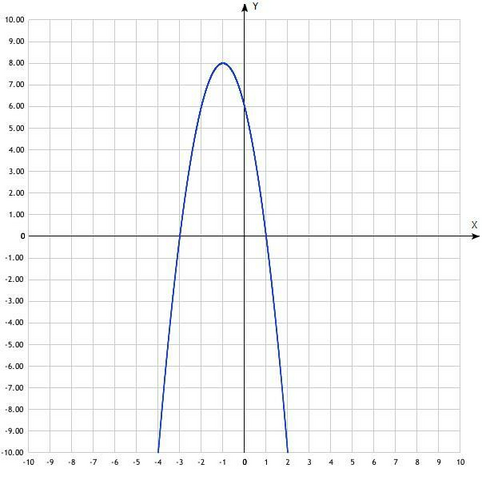
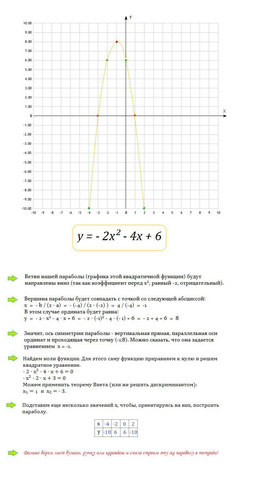
Сначала построим график функции 
(в первом файле - сам график, а во втором файле - этот же график, но с этапами построения).
Область значений функции - это все возможные значения, которые может принимать функция (то есть, те значения 
, при которых функция существует).
Отсюда следует, что область значений данной функции равна (это можно определить, посмотрев на график):
![\boxed {E(y) = (- \infty ; 8 \; ]}](https://tex.z-dn.net/?f=%5Cboxed%20%7BE%28y%29%20%3D%20%28-%20%5Cinfty%20%3B%208%20%5C%3B%20%5D%7D "\boxed {E(y) = (- \infty ; 8 \; ]}")
б).
Если мы посмотрим на график,то окажется, что:
- при
![x \in (-\infty ;-1 \; ]](https://tex.z-dn.net/?f=x%20%5Cin%20%28-%5Cinfty%20%3B-1%20%5C%3B%20%5D "x \in (-\infty ;-1 \; ]")
функция растет;
- при
функция убывает.
(В точке 
достигается точка максимума функции)
И ответ на задачу: функция возрастает на промежутке
![\boxed {x \in ( - \infty ; -1 \; ]}](https://tex.z-dn.net/?f=%5Cboxed%20%7Bx%20%5Cin%20%28%20-%20%5Cinfty%20%3B%20-1%20%5C%3B%20%5D%7D "\boxed {x \in ( - \infty ; -1 \; ]}")
