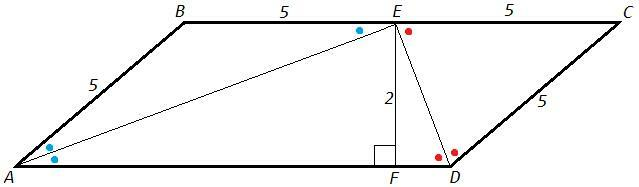
AE и DE - биссектрисы параллелограмма ABCD, точка E лежит на BC. Точка F лежит на AD, EF⊥AD. AB=5 см, EF=2 см.
Найти a) AD; б) S(ABCD).
-------------------------------------------------------------------
∠BAE=∠DAE (AE - биссектриса)
∠DAE=∠BEA (накрест лежащие при BC||AD)
∠BAE=∠BEA => △ABE - равнобедренный, AB=BE
Аналогично EC=CD
AB=CD=5 см, AD=BC (противоположные стороны параллелограмма)
a) AD =BC =BE+EC =AB+CD =5+5=10 (см)
б) S(ABCD) =AD*EF =10*2 =20 (см^2) (EF - высота)