При условии, что х≠1
Это гипербола. Асимптоты, которой:  .
.
Т.к. (-3), то гипербола будет во 2 и 4 четверти относительно новых асимптот. Область определения: (-∞;-2)∪(-2;1)∪(1;+∞). Это те значения х, которые может принимать график функции.
Область значений: (-∞;0)∪(0;1)∪(1;+∞). Это значения по оси у, которые имеет график.
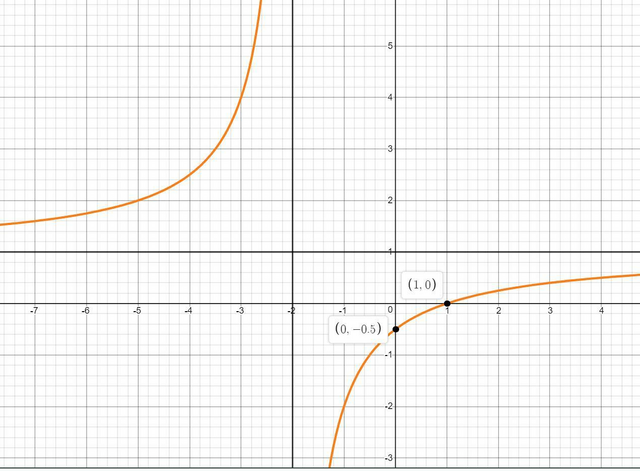
Найдём точки пересечения с осями:

Но при этом x≠1
Ответ: пересечение с осью x: нет
c осью у: (0;-0.5)
Если подставить x=1(в изначальное уравнение), то получается что мы делим на ноль, поэтому функция не определена в этой точке.