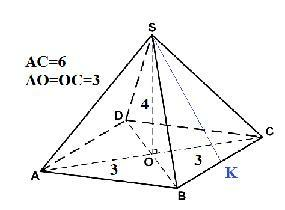
В основании пирамиды квадрат
Пусть сторона квадрата равна а.
Из прямоугольного треугольника АВС:
а=АС·sin45°=6·(√2)/2=3√2 см
Диагональ квадрата точкой О делится пополам.
АО=ОС=3
Значит,
Боковое ребро равно 5
Δ SOC - прямоугольный с катетами 4 и 3 ( египетский треугольник)
Апофема боковой грани SK=h
SK²=SC²-KC²=5²-(3√2/2)²=25-(9/2)=41/2
h=SK=√(41/2) cм
S(полн.)=S(бок.)+S(осн.)=(1/2)Р(осн.)·h+a²=
=(1/2)·4a·h+a²=2a·h+a²=
=2·(3√2) ·√(41/2) + (3√2)²=(6√41+18) cм²