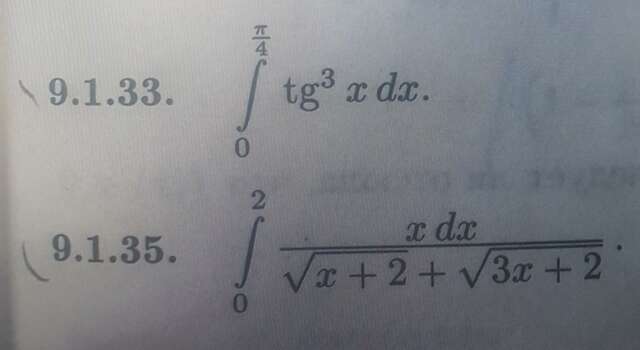Ребята, выручайте! Без Вас никак!Помогите разобраться в темеРешите и подробно распишите!Любую задачку, любое количество!За отдельную благодарность можете Всё, хочу на ваших решениях понять тему и научиться решать эти тяжки задачи! Надеюсь на Вас!Заранее огромное спасибо!Помоги :)