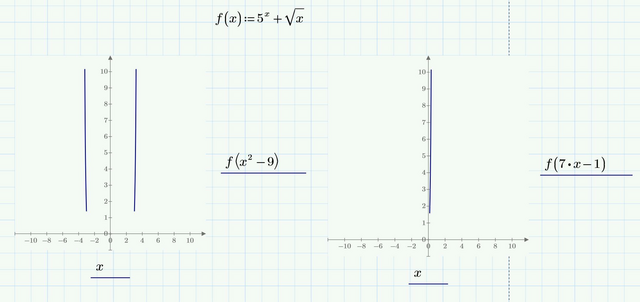
Пусть f(x)=5^(x) +√x
Уравнение:
f(7x-1)=f(x^2-9)
Очевидно ,что функция f(x) ,как и функции f(7x-1) и f(x^2-9) монотонны по области определения (x>=3). А значит у этих функций не могут быть одинаковые значения функции при разных значениях аргумента, то есть если 7x-1≠x^2-9 ,то f(7x-1)≠f(x^2-9)
Таким образом если решение существует,то оно удовлетворяет условию:
7x-1=x^2-9
x^2-7x-8
x1=-1 (не удовлетворяет ОДЗ)
x2=8
Ответ: x=8