Пошаговое объяснение:
Вопрос задачи найти не саму вероятность отказа, а число элементов, которые откажут с наибольшей вероятности.
Вычислим по формуле полной вероятности.
Вероятность отказа элемента - q = 0,2 - дана.
Вероятность работы - p = 1 - q = 0.8.
Для пяти независимых событий формула полной вероятности будет:
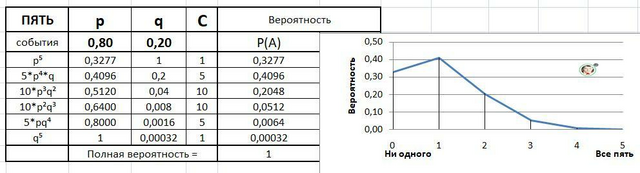
P(A) = (p+q)⁵ = p⁵+5*p⁴q+10*p³q²+10p²q³+5pq⁴+q⁵ = 1.
Коэффициенты можно вычислить по формуле Бернулли, но быстрее по "треугольнику Паскаля" - в приложении.
Расчет сведён в таблицу. Дополнительно и график функции вероятности.
Р(А) = 0,3277+0,4096+0,2048+0,512+0,0064+0,00032 = 1.
И вот по результатам (и графику) находим, что наиболее вероятен отказ одного элемента.
ОТВЕТ: Наибольшая вероятность отказа - одного элемента с р=0,4096.
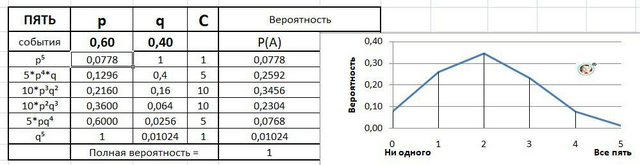
Дополнительно:
При вероятности отказа q = 0.4 наиболее вероятен отказ двух элементов. Рисунок в приложении.