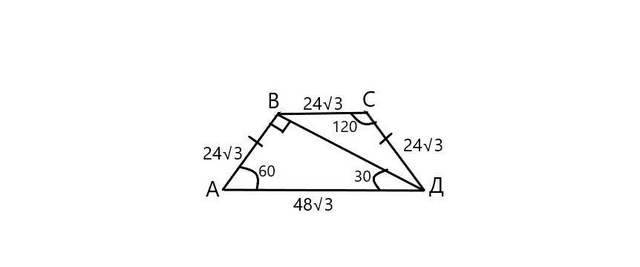
АВ=АД/2 (как катет лежащий против угла 30°) АВ=48√3/2=24√3; СД=АВ (трапеция равнобедренная); углы В и Д в треугольнике ВСД равны 30° (угол В в трапеции (180-60)=120°, угол В в треугольнике (120-90)=30°, угол Д в треугольнике (60-30)=30°); площадь трапеции равна сумме площадей треугольников АВД и ВСД; площадь треугольника равна половине произведения длин сторон на синус угла между ними.
S(АВД)=48√3*24√3*√3/4=864√3;
S(ВСД)=24√3*24√3*√3/4=432√3;
S(АВСД)=864√3+432√3=1296√3 ед².
Можно проще.
S(равнобедренной трапеции)=с*sinα(b-c*cosα), где b - основание , с - боковая сторона, α - угол при большем основании;
S=24√3*√3/2*(48√3-24√3/2)=36*36√3=1296√3 ед².
Еще можно через нахождение высоты, но думаю это лишнее.