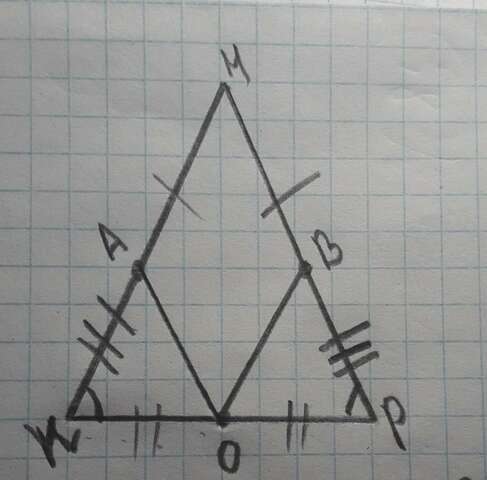** боковых сторонах МК и МР равнобедренного треугольника отложены равные отрезки МА и МВ....

Question

На боковых сторонах МК и МР равнобедренного треугольника отложены равные отрезки МА и МВ. Точка А и В соединены с серединой О основание треугольника. Докажите, что ОА=ОВ

Answer 1

Решение:

т.к. MA=MB, а MK=MP(как боковые), AK=BP

Т.к. точки A и B соединены с серединной точкой O, KO=OP

угол MKP=MPK(углы при основании равны)

Отсюда следует, что треуголники KAO и PBO равны по 1 признаку равенства треуголников (по двум сторонам и углу между ними), значит OA=OB

что и требовалось доказать.

---